This article is about a particular instrument we use in several of our radiological detection methods, the Gas Proportional Counter. Before I go into describing how it works and what it detects, I’ll briefly explain what I mean when I say “radiation.”
Radiation is any process where an atom emits some form of energy. This energy is emitted in the form of electromagnetic radiation (eg. Gamma rays) or as subatomic particles (eg. electrons, protons, neutrons, positrons). For the purposes of this article I’ll only mention three types of radiation: alpha decay, beta decay, and gamma decay.
An atom is usually described as a positively charged nucleus, which is a tightly packed bundle of positively charged protons and neutrally charged neutrons, surrounded by an orbital “cloud” of negatively charged electrons. This description isn’t perfect. We’re talking about the world of quantum mechanics, and you can’t actually see an electron or a proton because they don’t have a discrete location in space nor do they have a size or shape
(See: https://gravityandlevity.wordpress.com/2015/04/11/how-big-is-an-electron/).
In this world of quantum mechanics, everything is described with mathematics and nothing is intuitive. However, I’ll do my best to give you a mental model to work with.
Radiation comes from the nucleus- The tightly packed protons and neutrons held together by something called the “strong force” or the “strong nuclear force.” It’s one of the four fundamental forces (electromagnetism, gravity, strong force, weak force). The positively charged protons want to push each other away because they are all similarly charged. However, the “strong nuclear force,” which only works over incredibly short distances, overpowers this repulsive electromagnetic force and pulls the protons and neutrons together. Different atoms are defined and identified by their atomic number, the number of protons. For example, a carbon atom has 6 protons. But if you add a proton, it will become a Nitrogen atom. An atom’s mass number is the total number of protons plus neutrons.
For atoms with very high mass numbers, this bundle of protons and neutrons is large enough that the strong nuclear force, which as mentioned only works on very small scales, is no longer able to overcome the electromagnetic force trying to push the protons apart. The nucleus solves this problem by ejecting an alpha particle. An alpha particle is comprised of two protons combined with two neutrons. It is essentially a helium nucleus without the electrons. By ejecting an alpha particle, the nucleus becomes smaller and reduces the number of repulsive positive protons. This makes it so the strong nuclear force can hold together the nucleus more easily.
Beta decay is different and less easily explained. It’s caused by the “weak force” or “weak nuclear force.” It’s outside the scope of this article to go too deeply into the nature of the weak nuclear force. All you need to know is that, with beta decay, a proton is converted into a neutron and a positron (a positive electron) is emitted or, vice versa, a neutron is converted into a proton and an electron is emitted. Generally speaking, there’s a delicate balance of protons and neutrons in any given nucleus. If that balance is tipped in favor of too many neutrons, then an electron will be emitted. If the balance is tipped in favor of too many protons, a positron will be emitted. Since the atomic number (# of protons) changes during beta decay, the identity of the atom also changes. For example, Cs-137 will undergo beta decay and transform into Ba-137.
Gamma decay occurs when, after a particular decay event, the nucleus is still unstable. In these cases the excess energy is released in the form of a high energy photon called a gamma ray. To use Cs-137 as an example again, it’s often the case that after converting a neutron into a proton and releasing an electron, the nucleus of the newly minted Ba-137 is still in a high energy state. By emitting a gamma ray, the nucleus can release that excess energy and settle down.
That’s the basics of radiation.
PRINCIPLES OF OPERATION
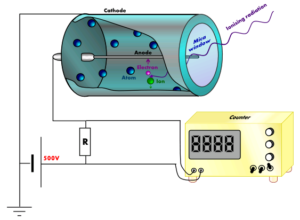
In our lab, the Gas Proportional Counter (GPC) is used to detect alpha and beta particles. The gas proportional counter is a device which can detect alpha and beta particles. GPCs come in many forms, but there are a few key design features that are consistent amongst them all. All GPCs feature a very thin, positively charged wire (anode) which is suspended across a gas filled, negatively charged chamber (cathode).
The fill-gas is typically a combination of a noble gas and a quenching agent such as methane (to be explained later). We use our GPC to detect the presence of alpha and beta emitting radionuclides in drinking water. We can do this by evaporating down an allotment of water until only the dissolved solids remain. This is done in such a way that the precipitated solids are coated evenly upon a stainless steel plate called a planchette. The planchette is placed in a slot underneath the GPC chamber so that the surface containing the precipitated solids is facing a window which exposes the inner chamber. When a decay event occurs, the alpha or beta particle will zoom through this window into the GPC chamber to be detected.
Let’s take a look at what happens when a particle enters the chamber. When an atom such as Th-230 undergoes alpha decay, the large, positively charged alpha particle erupts from the surface of the planchette and passes through the window into the gas filled GPC chamber. As the alpha particle moves through the chamber, it bumps into the atoms which make up the fill-gas. The positively charged alpha particle interacts with the negative orbitals of each gas atom through attractive coulomb forces. The kinetic energy of the alpha particle is then transferred to these orbital electrons (Knoll 30). As this occurs, many electrons are jostled and pulled away from the nuclei of the gas atoms (Knoll 42). In some cases, the electrons are merely excited to a higher orbital level before settling back down by releasing a photon. Sometimes, however, the electron is pulled off of the gas atom completely. The charge of an atom is determined by the balance of protons and electrons. If you remove one of those electrons, you leave behind an atom which has more protons than electrons. It then has an overall positive charge. This is called ionization. The result of this ionization process is a free electron and a positively charged gas ion.
A quick aside on the fill-gas.
Typically, argon is utilized for this roll because it is non-reactive, cheap, and has a relatively low electron attachment coefficient (Knoll 168). The emission of a photon, which occurs frequently, can sometimes cause secondary ionization events and lead to spurious counts. Methane is added in low amounts (10%) to soak up these extra photons and prevent this from happening (Knoll 167-168). This 90% argon and 10% methane gas combination is called P-10 gas. It’s a common fill gas used for gas proportional counters and it’s what we use in our lab.
Moving on.
An alpha particle is massive and energetic. It tends to travel in a straight line through the gas until it reaches the opposite side of the chamber. It plows through the argon atoms, leaving a trail of ion/electron pairs in its wake.
On the other hand, a beta particle is less massive. Since it is of a similar mass to argon’s orbital electrons, it tends to bounce around and takes a more tortuous path through the fill gas. Only rarely does it impart enough energy in one of these interactions to ionize anything (Knoll 43). As a result, alpha decay will result in a higher number of free electrons and ionized argon atoms than will beta decay. The importance of this effect will soon become clear.
Let’s take a look at what happens to the electrons and ions formed during alpha or beta radiation. Normally, the argon ions and free electrons would quickly recombine (Knoll 135). However, you will recall that this argon gas is contained within a negatively charged chamber with a thin, positively charged wire stretching through it. This separation of charges creates an applied electrical field. Due to this applied field, the negatively charged free electrons and positively charged argon ions will be pulled in opposite directions, the electrons towards the positively charged wire (the anode) and the positive argon ions towards the negatively charged chamber walls (the cathode). As these charges reach their respective electrodes (by electrodes I mean the wire and chamber walls), they reduce the applied voltage gradient (Knoll 148). This reduction in voltage gradient, or induced voltage change, is what the GPC detects and measures.
As the applied electrical field is made stronger, the ion pairs are separated more rapidly. This decreases the number of them which are able to recombine, increases the number which reach the electrodes, and causes the induced voltage change, detected by the instrument, to increase. Still with me? The induced voltage change will continue to increase along with the applied voltage until it reaches a point where recombination is prevented entirely. This is called the range of ion saturation. Within this range, any increase in applied voltage will no longer increase the induced voltage. All ionized argon atoms and free electrons will contribute to the final induced voltage change making the induced voltage proportional to the rate of ion formation. This is how ionization chambers work (Knoll 135).
What happens if we continue to increase the applied voltage gradient well past the ion saturation range?
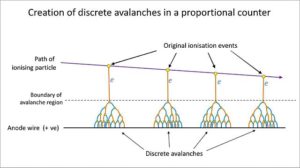
As we noted above, when applied voltage is increased, the electrons and argon ions move at a quicker and quicker rate towards their respective anode and cathode. Just like the alpha and beta particles, the electrons and argon ions will interact with the argon fill gas. While the massive, positively charged argon ions don’t move very quickly due to “size”, the free electrons are relatively light and fast moving. As the voltage gradient increases so does the kinetic energy of the electrons. Eventually, the electrons reach an energy level where they can ionize additional argon atoms, creating more electron / argon ion pairs. These newly formed pairs are also affected by the applied voltage gradient and join the original electron / ion pairs in drifting towards their respective electrodes. Assuming the applied voltage gradient is great enough, the newly formed electrons will ionize yet more argon atoms which in turn go on to ionize even more argon atoms (Knoll 159). This chain reaction is called a Townsend Avalanche. It serves to greatly increase the induced voltage change per original ionizing event. Due to the fact that the electrical field is strongest at very close radii to the anode wire, Townsend Avalanches preferentially occur in close proximity to the anode wire.
The size of the induced voltage change caused by a single electron is called the gas multiplication factor. If you know the gas multiplication factor for a particular applied voltage gradient, then you can calculate what the induced voltage change would be for multiple electrons (Knoll 169). This means that the induced voltage change is proportional to the number of original electron/argon ion pairs created by the incident radiation (Knoll 160-161). That’s why it’s called a gas proportional counter. If you recall, alpha and beta particles will ionize different numbers of argon atoms per decay. Since the induced voltage change is proportional to the number of ionized argon atoms, this gives us a rudimentary way to tell apart alpha and beta particles.
All of this is easier said than done. The electrical field around the thin wire anode changes drastically depending on the thickness of the wire and the gas multiplication factor increases or decreases near-exponentially with an increase or decrease in the strength of the applied electrical field. Due to these factors, the wire must be uniformly thin all along its length and the gas proportional counter must be operated at an extremely stable voltage (Knoll 170).
Additionally, there are secondary ionization events, alpha-beta crossover, backscattering, self-absorption, and other side-effects which can cause inefficiencies. This is what I’ll talk about in the next section.
Set up
Our goal in the lab is to translate the data produced by the GPC, counts per minute and induced voltage change, into alpha or beta specific picocuries per liter.
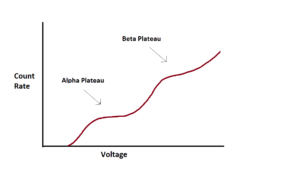
Our first step is to know how powerful our applied voltage needs to be. We determine exactly what our applied voltage should be by running what’s called a voltage plateau. We place a high activity combined alpha / beta emitter into the GPC and count for a set amount of time across a range of voltage gradients, starting at 0V and working our way up to 2000V. The GPC will measure count rate and we graph that count rate against the voltage. The graph will look something like this:
As the voltage increases, the counts per minute (cpm) increases as well up to a certain point, then it levels off. This area is the alpha plateau. It’s similar to the ion saturation range mentioned earlier. At this voltage, all alpha decays are triggering Townsend Avalanches so that increasing the voltage slightly further won’t increase count rate. However, if you continue to increase the voltage you’ll eventually see the cpm start to increase again. This rise comes from the beta decay. Because beta particles are less massive than alpha particles, it takes a larger voltage gradient to instigate ionization events. The beta cpm will also reach a beta plateau, albeit a less well defined one. It is less defined due to the fact that the induced voltage change caused by beta particles is more variable than induced change caused by alpha particles (Knoll 185). If we’re counting just alpha particles, then we will use the alpha plateau. However, you can use the beta plateau to count both alpha and beta particles. Typically we try to pick a voltage as close to the “knee” of the curve as possible. That’s because we want our gas multiplication factor to be as low as possible in order to reduce background noise and prevent spurious counts (Knoll 184).
Now that we’ve set our GPC voltage, we’re ready to count. In the simplest case, we will just evaporate away an allotment of water until only the dissolved solids remain, coated evenly across a stainless steel planchette.
After counting, we take our data and punch it into the following equation:
Net cpm / (efficiency x Volume x 2.22).
Net cpm is the cpm after background is subtracted out. All the time, cosmic rays are pouring down from space and, occasionally, one of them passes through our GPC and ionizes an argon atom which can lead to non-alpha or beta induced Townsend Avalanches. This happens at a constant rate, so we are able to simply count an empty planchette to calculate the background cpm. Then, after we count our sample, we know to subtract this background cpm from our raw cpm to get an accurate net cpm.
We take this net cpm and divide it by efficiency (which I’ll explain soon), volume used, and 2.22. By dividing by the volume we evaporated down, we can convert our result into liters. We divide by 2.22 in order to convert our net cpm into picoCuries (2.22 cpm = 1 pCi).
The efficiency is a factor which tells us what % of total disintegrations will be detected by the GPC. Take into consideration the fact that, although alpha and beta decay is equally likely to launch a particle in any direction, that particle only gets detected if it is launched into the GPC chamber. This depends on geometrical factors. For example, only particles launched from the side of the planchette facing the GPC chamber can enter through the window to be counted, so right off the bat our efficiency is down to 50%. In fact, geometrical issues can diminish the efficiency down to around 30% (Semkow 570). Besides just the geometrical efficiency, there’s also the issue of self-absorption. Some of the alpha and beta particles get blocked from entering the GPC chamber by the solid precipitate matter which is layered upon the planchette. This can decrease the efficiency even more, until we reach levels as low as 20% or even 10%.
Our inefficiencies can also go in the other direction. Although planchette/GPC geometry and self-absorption might diminish the efficiency, there’s something called backscattering which can increase it erroneously. Backscattering happens when a beta or alpha (but usually beta) particle is ejected in the direction of the planchette, but then bounces backwards off of it and into the GPC detection chamber. This happens with high energy beta emitters such as Sr-90/Y-90. Besides backscattering, some emitters, Cs-137 for example, undergo something called internal conversion (Semkow 570). This is caused when, after the emission of a beta particle, the nucleus is still not entirely stabilized. Usually in this situation, a gamma ray is ejected. However, sometimes the energetic nucleus will kick off an electron instead. This conversion electron can enter the GPC and be counted as a beta particle, even though it is not. This will also erroneously increase the efficiency (Semkow 570).
Our solution to these problems are simple. Let’s use a beta emitter, Cs-137, as an example. We take a known amount of Cs-137, and we coat it onto several planchettes, each with a different amount of absorbing solids. Since we know exactly how much of the Cs-137 we added to the planchet, we know the rate at which it will emit beta particles. By comparing this predicted rate against the actual net cpm recovered from the GPC, we can determine our % efficiency. By doing this over a range of weights, we can plot weight against efficiency. By weighing sample of unknown activity, we can figure out what % efficiency to use in our calculation.
This works great – on the condition that you know you are counting Cs-137. As it turns out, different beta emitters eject beta particles at different velocities, called the decay energy. Decay energy appears to be roughly proportional to efficiency. Sometimes you have no idea what type of radionuclide you are counting and therefore have no idea which efficiency to use in your equation. Other times, you do know which radionuclide you are counting, but if the radionuclide has a very short half-life then it is not conducive to running an efficiency experiment. We have this problem with our Ra-228 method. With this method, we determine the level of Ra-228 by measuring Actinium-228 content. Unfortunately, Ac-228 has a half-life of about 7 hours and won’t survive long enough to run a full efficiency experiment.
Our imperfect solution to this problem is to plot an efficiency curve with an emitter of similar decay energy but with a longer half-life. In our lab, we use Sr-89 to extrapolate the Ac-228 efficiency. Once we have the Sr-89 efficiency, we can multiply it by a factor which represents the difference between decay energies (Ac-228’s decay energy is about 70% of Sr-89’s).
We’re still not done!
As mentioned previously, we can tell apart alpha and beta emitters based on the change in induced voltage. Alpha particles tend to cause a pretty uniform induced voltage change. This is because they travel in a straight line and ionize a fairly standard number of argon atoms. Beta particles, on the other hand, take highly variable paths through the gas (lower energy particles take longer to get through and therefore take the highest variation of paths). Because of these variable paths, the induced voltage change can vary much more than the alpha. We determine whether a particular Townsend Avalanche was caused by an alpha or beta particle by looking at the size of the induced voltage change caused by each original ionization event. We consider all induced voltage changes within a certain range to be beta counts and all induced voltage changes within a higher range to be alpha counts.
It’s common that an alpha emitter will cause secondary emissions such as conversion electrons (mentioned earlier), auger electrons (when a higher orbital electron drops down to fill a lower level vacancy, occasionally it releases enough energy to knock off another electron), or x-rays. These all get counted in the GPC and are similar in energy to beta particles. This means that if you’re trying to count beta particles in the presence of an alpha emitter, you will get erroneous beta counts (Semkow 571).
We partially solve this problem by counting an alpha emitter alone at the beta plateau and count the number of counts which are registered as beta. Since we know there isn’t a beta emitter in our test sample, we use the erroneous beta counts to determine % crosstalk. This isn’t perfect, however, since different alpha emitters will be accompanied by a unique proportion of secondary emissions and will cause different % crosstalks (Semkow 571). If you don’t know which alpha emitter is in your sample to begin with, you won’t know which % crosstalk to use in your calculations.
That’s how a Gas Proportional Counter works! If you have any questions, feel free to e-mail me: [email protected]
Thanks for reading!
Knoll, Glenn F.. Radiation Detection and Measurement. New York: John Wiley & Sons, Inc., 2000
Semkow, Thomas M., and Pravin P. Parekh. “Principles of Gross Alpha and Beta Radioactivity Detection in Water.” Health Physics 81.5 (2001): 567-74