Introduction
This is a description of JakeTacToe 2.0, the intended improvement to JakeTacToe 1.0. The point of this article is to guide somebody (including myself) through the JakeTacToe 2.0 code so that it can be understood and/or updated.
This project didn’t turn out as well as I expected. I underestimated how much time it would take and started to burn out with the Tic Tac Toe Learning concept. As my interest waned, I pushed harder towards completion, accepting imperfect solutions in the interest of finishing quickly. This inevitably led to poorly structured code and a project that was “just good enough.” Not my proudest moment. That being said, the main purpose of JakeTacToe was to learn, and failure teaches just as well as success.
Organizational mistakes made this project more difficult than it had to be. I plan on talking about those next time. This article, however, is just about JakeTacToe 2.0; What it does, how it works, and what I could have done to make it better.
I’ve written each section in two parts. The first part is a non-technical description. The second part (formatted differently) is a technical description which guides you through the actual code. If you’re going to read the technical description, then you’ll need to see the jtt2.py file from the source:
If you’re not a technical person and just want to get a feel for how JakeTacToe 2.0 works, then you can skip the technical parts.
Game Engine
I used similar game engines for JTT1 and JTT2. A Tic Tac Toe game board can be constructed by building a 2 dimensional array (‘list’ in Python lingo).
[
[ “[ – ]”, “[ – ]”, “[ – ]” ],
[ “[ – ]”, “[ – ]”, “[ – ]” ],
[ “[ – ]”, “[ – ]”, “[ – ]” ]
]
As you can see, it’s just 3 lists nested within another list. Each inner list contains 3 strings,
“[ – ]”, which represent the spaces on a 3×3 grid.
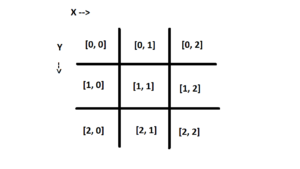
By printing this with my Engine.print_grid() function, a graphical interface can be displayed for human reference. More conveniently, I can refer to specific spaces on the game board by using indexes ( grid[y][x] or [y, x] ). For example, grid[1][1] refers to the center “[ – ]”. Grid[2][0] refers to the bottom left “[ – ]”.
When a player chooses a space, the engine replaces “[ – ]” with “[ X ]” or “[ O ]” and updates a few game engine attributes to keep track of which spaces are available and which are claimed. There are separate functions which determine wins, losses, and draws.
Remember, for these sections you’ll want to have the JakeTacToe 2.0 source code opened in another tab(JakeTacToe 2.0 Github). Refer to it as you follow along here. There are two classes, Player and Engine. When the JakeTacToe script is called, two Player objects are instantiated (one for each player). The Player class contains a bunch of methods and attributes related to learning. For now, just take note of: Player.symbol: The “X” or “O” which represents the player. Player.owned: The indexes ( [y, x] = grid[y][x] ) which represent the spaces the player has already claimed. These two newly created Player objects are then passed to the Engine constructor to instantiate an Engine object, called ‘game’ in my code. The Engine object contains methods necessary for running a game and the following attributes: Engine.grid: The two dimensional array which contains strings meant to graphically represent the Tic Tac Toe game board Engine.winning_sets: The grid index sets which, if owned by player, represent a win (3 in a row) Engine.available: The grid indexes which point to spaces unclaimed by either player To play a game, the Engine.play_game() method is invoked. Engine.play_game() first opens connections to the database using the Player.open_connection() method for each player and then initializes some attributes, Player.previous_layer, Player.new_patterns, and Player.total_game_patterns. These attributes will be used later by the Player methods. Once the player’s attributes are initialized, we enter a while loop. The while loop will first print the grid using Engine.print_grid() which prints the grid list to the terminal in a human readable format. Next, it will invoke Engine.play_round(). Engine.play_round() accepts two arguments, the player object whose turn it is and a boolean which determines whether the player will make a move randomly (Set to False) or if the player will make a competitive move (Set to True). First the computer player’s move will be decided (either randomly or competitively as described above). Once the player has provided its move, the Engine.grid, Engine.available, and Player.owned attributes are updated to reflect the changes triggered by this move. Finally, a couple of learning methods are invoked. I’ll cover those soon. After Engine.play_round(), the Engine will check if the player has won by using Engine.check_for_win which simply sees if Player.owned matches any of the sets in Engine.winning_sets. If so, the loop is broken, a learning method is invoked, and the game ends. If not, Engine.check_for_draw() checks for a draw by seeing if Engine.available is empty. If so, the game ends. If not, the Engine prints the grid again and repeats the process for the other player. This continues until the game ends in a win or a draw.
Intent
In JTT1, all learning was facilitated by sqlite3 database interactions. Each board position was saved as a descriptive position ID. Each available move for a particular position had an individual weight and the computer would pick the highest weighted move.
The computer player would keep track of each board position and remember the move made in said position. If the player won, the weight for that move would increase and if the player lost the opposite would happen. After many games, good moves would have high weights and would be chosen. Bad moves would have low weights and would not be chosen. This was enough to create competitive computer players.
It all worked well despite an important caveat; This learning process required the exhaustive exploration of each of the 4520 possible board positions. Some of those positions had to be seen several hundred times for the winning moves to increase significantly in weight above losing moves. Since many board positions were only seen 7% of the time, it took almost 100k games for the computer to play competitively.
I tried to take a different direction in JTT2. Broadly speaking, my goal was to create a learning algorithm which could be transplanted into several different game engines (such as a checkers game or a chess game) and improve more quickly than JTT1. In order for this to be possible, JTT2 had to learn by a means which did not make it necessary to see each position multiple times. It also had to be generic enough to be transplanted into another game engine and work the same way.
I decided it would be a better learning experience if I attempted to figure out a way to do this on my own without resorting to using somebody else’s learning algorithms and strategies. Things started out promising. I came up with a pattern recognition system which I hoped could be useful in detecting the similarities between each winning position. In this way, the computer player could apply a common set of strategies against several analogous positions.
It was about this time that I realized how long it was going to take me to finish this monstrosity. I was already sick and tired of Tic Tac Toe and felt ready to move on to a new project which might actually be useful to somebody. Afterall, if I’m going to be spending so much time working on something, shouldn’t it at least be useful? This is where things began to fall apart. I had a choice between dropping the project completely or modifying the goal to make it attainable. I chose the latter.
My new, more reasonable goals for my computer player were as follows:
-Learn to play Tic Tac Toe competitively in fewer than 10k game repetitions
-Adopt a functionality which allows the computer player to recognize and represent positions more complex than just 3 in a row on grids larger than 3×3. For example, I would like the computer to be able to recognize a diamond shape anywhere on a 12×12 grid.
As much as I felt like a hack for simplifying my goals, I also felt a breezy sense of relief. This was now a manageable project which I could finish quickly and move onto something else without feeling like a quitter.
Spoilers, I was only partially successful on both accounts.
The computer will play relatively competitively after 1000 games, but it cannot beat me. It will win against an opponent choosing moves at random (96% of the time if it goes first and 84% of the time if it goes second).
The computer cannot recognize diamonds on large grids like I planned. However, it can recognize all of the ‘3 in a row’ patterns and will adapt if I remove a winning position (ie, if ‘3 in a row’ diagonally no longer won games, the computer would adjust and no longer attempt to build diagonal ‘3 in a rows’). That being said, the way I built the pattern recognition framework could potentially make that sort of functionality possible. I’ll talk more about that in the next section.
In the end, I have a group of functions which can play ~1000 games of Tic Tac Toe (much less than the 10k that I originally planned on) and, pitted against an opposing player choosing moves at random, win a majority of the time.
Pattern recognition
What makes JakeTacToe 2.0 different from 1.0 is the pattern recognition capability. This is the process through which the computer player recognizes and labels the patterns which appear upon the Tic Tac Toe grid. It is the core of JTT2 and is handled by a couple of functions which ultimately produce a list of descriptive position patterns. I’ll explain how in a second, but first I should define what I mean by position patterns.
Here’s an example of a position pattern:
[[1, 1], [‘horizontal’, [‘E’, ‘+’, ‘-’]]]
It has the form:
[[y, x], [‘orientation’, [‘adjacent-symbol’, ‘center-symbol’, ‘adjacent-symbol’]]]
As you can see, it’s just a nested list.
As I explained earlier, the grid is composed of a two dimensional array; 3 lists, each containing 3 strings, “[ – ]”, “[ X ]”, or “[ O ]”, all within a higher level list. Each space on the grid can be specified by its list index. For example, grid[0][0] would point to the first item on the first list which would be the space in the upper left corner.
As you may have guessed, [y, x] represents the indexes for a specific space (ie, grid[y][x]). It is essentially pointing to one of the spaces on the Tic tac toe grid. The second item in the position pattern, [‘orientation’, [‘adjacent-symbol’, ‘center-symbol’, ‘adjacent-symbol’]] describes the contents of that space as well as the content of two adjacent spaces determined by ‘orientation’.
That may not be clear, so I’ll give an example:
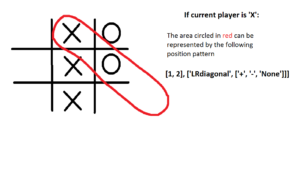
Let’s take that position pattern from earlier, [[1, 1], [‘horizontal’, [‘E’, ‘+’, ‘-’]]].
This position pattern is describing the horizontal row with respect to the grid[1][1] space. The [‘E’, ‘+’, ‘-’] represents the contents of those 3 spaces. In other words, this position pattern represents: [‘space to the left of grid[1][1]’, ‘grid[1][1] space’, ‘space to the right of grid[1][1]’]. ‘E’ means the space is empty, ‘+’ means the space is occupied by the current player’s symbol (X or O), and ‘-’, means the space is occupied by the opposing player. Alternatively, it could also show ‘None’, which would mean that there is not a square in the specified location (for example, there’s nothing to the left of, nor above, the space in the top left corner).
If instead the position pattern was [[2, 0], [‘vertical’, [‘+’, ‘+’, ‘None’]]], it would be describing the vertical column with the bottom left space as its center where both the bottom left space and center left space are filled with whichever symbol represents the current player.
See the following diagram for further clarification.
The Tic Tac Toe grid can be represented by a list of position patterns. This is how the computer represents the current state of the game grid.
As mentioned in the ‘Intent’ section, one of my goals was to create a way to represent complex patterns. This pattern recognition technique is potentially capable of doing this, although it is not fully fleshed out. I imagined some algorithm which could reduce a complex shape into a unique group of position patterns which could then be targeted by a regular expression.
For example, if 3-in-a-row can be described as,
[[*, *], [‘*’, [‘+’, ‘+’, ‘+’]]]
(note: the * are wildcards which represent any of the available options)
then more complicated shapes, such as a right angle, could be represented by the concurrent appearance of:
[[y, x], [‘horizontal’, [‘*’, ‘+’, ‘+’]]]
AND
[[y, x], [‘vertical’, [‘*’, ‘+’, ‘+’]]]
OR
[[y, x], [‘horizontal’, [‘+’, ‘+’, ‘*’]]]
AND
[[y, x], [‘vertical’, [‘*’, ‘+’, ‘+’]]]
…and so on.
This functionality hasn’t been worked out, but with some time and effort I could at least see a way forward.
A list of position patterns is returned each turn in order to represent the current state of the TicTacToe grid.
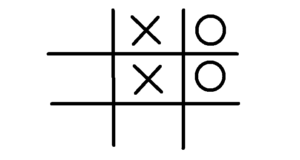
For example, take the position:
After the pattern matching functions run, it will return the following list:
[
[[0, 0], [‘RLdiagonal’, [‘None’, ‘E’, ‘None’]]],
[[0, 0], [‘horizontal’, [‘None’, ‘E’, ‘+’]]],
[[0, 0], [‘LRdiagonal’, [‘None’, ‘E’, ‘+’]]],
[[0, 0], [‘vertical’, [‘None’, ‘E’, ‘E’]]],
[[0, 1], [‘RLdiagonal’, [‘None’, ‘+’, ‘E’]]],
[[0, 1], [‘horizontal’, [‘E’, ‘+’, ‘-‘]]],
[[0, 1], [‘LRdiagonal’, [‘None’, ‘+’, ‘-‘]]],
[[0, 1], [‘vertical’, [‘None’, ‘+’, ‘+’]]],
[[0, 2], [‘RLdiagonal’, [‘None’, ‘-‘, ‘+’]]],
[[0, 2], [‘horizontal’, [‘+’, ‘-‘, ‘None’]]],
[[0, 2], [‘LRdiagonal’, [‘None’, ‘-‘, ‘None’]]],
[[0, 2], [‘vertical’, [‘None’, ‘-‘, ‘-‘]]],
[[1, 0], [‘RLdiagonal’, [‘+’, ‘E’, ‘None’]]],
[[1, 0], [‘horizontal’, [‘None’, ‘E’, ‘+’]]],
[[1, 0], [‘LRdiagonal’, [‘None’, ‘E’, ‘E’]]],
[[1, 0], [‘vertical’, [‘E’, ‘E’, ‘E’]]],
[[1, 1], [‘RLdiagonal’, [‘-‘, ‘+’, ‘E’]]],
[[1, 1], [‘horizontal’, [‘E’, ‘+’, ‘-‘]]],
[[1, 1], [‘LRdiagonal’, [‘E’, ‘+’, ‘E’]]],
[[1, 1], [‘vertical’, [‘+’, ‘+’, ‘E’]]],
[[1, 2], [‘RLdiagonal’, [‘None’, ‘-‘, ‘E’]]],
[[1, 2], [‘horizontal’, [‘+’, ‘-‘, ‘None’]]],
[[1, 2], [‘LRdiagonal’, [‘+’, ‘-‘, ‘None’]]],
[[1, 2], [‘vertical’, [‘-‘, ‘-‘, ‘E’]]],
[[2, 0], [‘RLdiagonal’, [‘+’, ‘E’, ‘None’]]],
[[2, 0], [‘horizontal’, [‘None’, ‘E’, ‘E’]]],
[[2, 0], [‘LRdiagonal’, [‘None’, ‘E’, ‘None’]]],
[[2, 0], [‘vertical’, [‘E’, ‘E’, ‘None’]]],
[[2, 1], [‘RLdiagonal’, [‘-‘, ‘E’, ‘None’]]],
[[2, 1], [‘horizontal’, [‘E’, ‘E’, ‘E’]]],
[[2, 1], [‘LRdiagonal’, [‘E’, ‘E’, ‘None’]]],
[[2, 1], [‘vertical’, [‘+’, ‘E’, ‘None’]]],
[[2, 2], [‘RLdiagonal’, [‘None’, ‘E’, ‘None’]]],
[[2, 2], [‘horizontal’, [‘E’, ‘E’, ‘None’]]],
[[2, 2], [‘LRdiagonal’, [‘+’, ‘E’, ‘None’]]],
[[2, 2], [‘vertical’, [‘-‘, ‘E’, ‘None’]]]
]
Player.build_pattern_list() is responsible for building the list of position patterns. It does this by calling Player.test_around() for each location on the tic tac toe grid. Player.test_around() first builds a dictionary called ‘surround.’ There’s a long if/elif chain which links the relative position of each space (above, below, top_left, etc) to a grid index (grid[y][x]). This gets slightly tricky because some locations are on the edge of the grid and therefore certain adjacent spaces don’t exist. For example, there’s nothing above the top-left space so it cannot be targeted using indexes. Once the ‘surround’ dictionary gets sorted out, another dictionary called ‘angles’ is created. This is where the positions in ‘surround’ get sorted into the orientations specified by the position patterns. For example, surround[‘above’], surround[‘main’], ,and surround[‘below’] get sorted into the ‘vertical’ orientation. Finally, ‘angles’ gets standardized into its final form so that any symbol matching the current player gets labeled as a ‘+’, any symbol matching the opposing player gets labeled as a ‘-’, any symbol matching an empty space gets labeled as an ‘E’, and any non-existent space gets labeled as ‘None’. Player.test.around() returns the final ‘angles’ dictionary. Player.build_pattern_list() fills up a list called test_around_result with the grid index locations and the ‘angles’ dictionary returned for each. This test_around_result list is ultimately broken down into 3 separate formats, layer 1 through layer 3. Layer 3 is the position pattern I’ve been describing thus far. Layer 2 is just the [‘orientation’, [‘E’, ‘E’, ‘E’]] part. And Layer 1 is just the [‘E’, ‘E’, ‘E’] part. For the time being, I’m only using layer 3, but originally I thought I would make use of all 3 layers. I’ve kept Player.build_pattern_list() the way it is in case I see a reason to use one of the alternative layers in a future incarnation of JakeTacToe.
Narrowing down winning Position Patterns
Each turn, the computer player generates a list of position patterns and keeps track of any new ones which have arisen. When the conditions for winning have been met, the game engine notifies the computer player that it has won, and the player will add all of the new position patterns from that turn to a ‘winning positions’ list which gets saved to the sqlite3 database. One (or many) of the position patterns on this list is responsible for the win, however the computer is unable to tell which one it is since there are also innocuous position patterns mixed in amongst the winning ones.
In order to separate out the winning vs non-winning position patterns, the computer will compare all patterns on the ‘winning positions’ list against all patterns on another list called the ‘total game patterns’ list. The ‘total game patterns’ list is also stored on the sqlite3 database and keeps a running tally of all of the position patterns which have ever appeared in a game without triggering a win. If a position pattern appears on the ‘total game patterns’ list, it means that it has appeared before without triggering a win and, therefore, is not essential to winning a game. These patterns are removed from ‘winning positions.’ Eventually, only those position patterns which lead to a win 100% of the time remain on the ‘winning positions’ list.
The computer player now has a database full of winning positions. It just needs to learn how to build them.
Note: I mentioned in the previous section that I could group together position patterns to represent more complex patterns. If I were to move forward on this, it is this section which would have to be overhauled.
After each win, the method Player.find_winning_pos() is called. This is the method responsible for determining which position patterns trigger a win 100% of the time. At the beginning of the Engine.play_round() method (before the player makes his move), Player.tgp_function() is invoked. This method builds a pattern list with Player.build_pattern_list and then appends those position patterns, if they’re not already appended, to the player’s total_game_patterns attribute. Then, the database is updated to reflect this new total_game_patterns list. At the beginning of each game, the database’s version of total_game_patterns is pulled and appended to the player’s version of total_game_patterns. Total_game_patterns is supposed to be a list of all position patterns which do not cause Engine.check_for_win() to signify a win. For this reason, it’s important that Player.tgp_function() is invoked before the computer player makes its move because it’s possible that this move would create a winning position pattern. If Player.tgp_function() runs in between the creation of this winning position pattern and Engine.check_for_win(), then a winning position pattern would be appended to total_game_patterns and that would totally defeat the purpose. Once the player makes his move and the game attributes are updated, Player.new_pattern_function() is invoked. Timing is everything with this method. At the beginning of the game, Player.new_patterns and Player.previous_layer are both initialized to equal the list of position patterns for the empty grid. When Player.new_pattern_function() is invoked, first Player.new_patterns is deleted. Then a new list of position patterns is created with Player.build_pattern_list(). All of the patterns on this list which are not also on the Player.previous_layer list are appended to Player.new_patterns. Next, Player.previous_Layer is deleted and then recreated as the list of position patterns describing the current game board. This attribute will be used again next turn when player.new_pattern_function() is called once more. Player.find_winning_pos() first pulls the database’s version of total_game_patterns (this is a redundant step which I’ve left in because...whatever, it works. I could probably just use the player’s version of total_game_patterns). It also pulls the ‘winning patterns’ list from the database and combines it with the Player.new_patterns attribute. This newly updated Player.new_patterns list is compared to total_game_patterns and any pattern which also appears on total_game_patterns is removed from Player.new_patterns. I repeat this loop 4 times because, for some reason, it wasn’t removing all of the non-winning Player.new_patterns. Repeating the loop several times fixed the problem. Not very elegant, but it got the job done. Once Player.new_patterns has been whittled down, it is uploaded to the database as the new ‘winning patterns’ list.
Learning cause and effect
With a list of winning positions in the database, the computer player needs to learn how to create them from scratch.
The computer makes a move by choosing one of the position patterns which have empty spaces available. [[1, 1], [‘Horizontal’, [‘E’, ‘E’, ‘+’]]] has spaces available.
[[2, 0], [‘Vertical’, [‘+’, ‘+’, ‘None’]]] does not. Once it has decided upon a position pattern, it chooses one of the empty spaces and refers to it by index (The index, in this case, is targeting an item in the [‘E’, ‘E’, ‘+’] list). For example, if it wanted to pick the left space from position pattern [[1, 1], [‘Horizontal’, [‘E’, ‘E’, ‘+’]]], it would use an index of 0.
Over the course of many games, the computer player continually updates the sqlite3 database with information about which moves it has made and the new patterns which arose subsequently to that move. It will eventually have enough information to be able to predict with 100% accuracy which position patterns will appear after a particular move has been made.
Now the computer player has narrowed down all of the winning positions and it knows how to create new positions. Time to put it all together.
At the end of Engine.play_round(), after the computer player has decided upon its move by picking a position pattern / index combo, as described above, Player.update_chain() is invoked. Player.update_chain accepts as arguments the position pattern, index, and Player.new_patterns list. This method’s purpose is to update the database table which I’ve decided to call ‘Chain’. ‘Chain’ has records which link up the position pattern / index combo (in the form of[position_pattern, index]), the list of resulting patterns where each resulting pattern is of the form [position_pattern, # of times appeared], times chosen which is simply the number of times that position pattern / index combo has been chosen, and top patterns which are the resulting position patterns which appear greater than 99% of the time that the position pattern / index combo has been chosen. First, the record is pulled from the ‘Chain’ table for the position pattern / index combo chosen by the player. Then, the resulting patterns for that record is compared to the Player.new_patterns list and any new pattern which is also in the resulting patterns list is updated by increasing the # of times it has appeared by 1. If the new pattern is not already represented on the list, it is added. Next, the top patterns are decided by dividing the # of times a resulting pattern has appeared by the # of times a position pattern / index combo has been chosen. If that number is > 0.99 (or 99%), then that resulting pattern is added to the top patterns list.
Competing
We have the 3 pieces to our puzzle. The computer can create a list of position patterns to describe the board, it knows which position patterns would trigger a win, and it knows how to create those patterns.
During a competitive game, the computer will draw from the database its list of winning positions and all of the move data which it has accrued over the course of many practice games. Using the move data, the computer player will construct a list of all the position pattern/index combos which it knows will lead to the appearance of each winning position. It will compare this list against the list of position patterns which currently represent the Tic Tac Toe grid. If it finds a match, it will make that move and create the winning position. However, if it cannot find a match, it will construct a new list. This time, the list will contain all of the moves which would create each of the leading position patterns from the previous list to appear. Then it will compare this new list against the current grid’s position pattern list. This process repeats itself until it finally finds a match.
Here’s a typical round:
- The computer pulls the list of winning positions from the database.
- For each position pattern on the winning positions list, the computer determines which position pattern/index combo would lead to that winning position. It generates a list of these leading moves.
- The computer compares this list of leading moves to the current grid’s list of position patterns. If it finds a match, the computer will choose it. If it finds multiple matches, the computer will choose the move which leads to the highest number of winning positions to appear.
- If it does not find a match, it will generate a new list of leading moves, this time for the position patterns/index combos which lead to each position pattern on the previous leading moves list.
- It again compares the leading moves list to the current grid. If it finds a match, it chooses the move which leads to the highest number of the previous leading position patterns appearing.
- This cycle repeats until a match is found. It happens every turn.
As I mentioned in an earlier section, the Engine.play_round() method accepts as an argument a boolean which specifies whether the player will make its move randomly or competitively. If this boolean is set to False (randomly), the position pattern and index combo will be chosen at random. This is handled by the Player.random_move() method. This method accepts a list of position patterns as an argument. These position patterns have been produced by Player.build_pattern_list() and preprocessed by Player.validate() which removes all position patterns without an available space to choose from (any position patterns without an ‘E’). Player.random_move() chooses one of the position patterns at random and then chooses one of this position pattern’s empty spaces at random as well and returns these choices to be used by Engine.play_round(). If the boolean is set to True (compete), then the position pattern / index combo is returned by the method Player.compete(). This method will pull the ‘winning position’ list from the database and build a list of position patterns with Player.build_pattern_list(). It will then pass these two lists to the method Player.find_leads(). Player.find_leads() is admittedly a very hacky and convoluted function. It starts out simply enough; It loops through the ‘winning positions’ list and pulls all of the position pattern / index combos from the ‘Chain’ table where the ‘winning position’ pattern is contained in the Top Pattern list of that particular record. Remember that Top Pattern’s are the patterns which appear > 99% of the time when a particular position pattern / index is chosen. Once this list of leading patterns has been assembled, it is cross referenced against the current grid’s position pattern list. If there is no match, then Player.find_leads() is called again, this time the newly assembled leading patterns list is passed in place of the ‘winning positions’ list. If there is a match (or multiple matches), then it would be advantageous for the method to return a position pattern / index combo that leads to as many of the positions on that ‘winning positions’ list(or leading patterns list if the first round didn’t have any matches with the grid position pattern list). This is where it gets convoluted. First, the position_pattern /index combos are all converted by the Player.choose() method into the matrix indexes specified by the particular position_pattern /index combos. Matrix indexes are, if you’ll remember, the [y, x] coordinates which point towards a particular grid space. Now, I want to choose from this list the matrix index which appears most often. Since this matrix index exists as a list, it took some hackery to get this to work. No doubt there’s a better way to do this. But as I’ve mentioned, I just wanted to get it to work as quickly as possible. I opted to use the Counter module which takes a list of items and returns a dictionary which specifies the # of times each item appears on the list. This required me to convert the matrix index list into a list of strings with stringify() (since the Counter module doesn’t work with lists), utilize the Counter module to find the matrix index (or indexes) which appeared most often and add it/them to a list, convert this list from strings back to lists with destringify(), find all of the position_pattern / index combos which pointed towards these matrix indexes, choose one of those at random, and then return that combo. Once Player.compete() had this position_pattern / index combo, it would return it back to Engine.play_round() and the program would move forward. If anything went wrong and no position pattern / index combo was returned from Player.find_leads(), then a position pattern / index combo would be chosen at random and returned.
Conclusion
The previously described 3 part strategy creates a computer player which, after about 1000 games (possibly less), will win against a competitor, playing randomly, the majority of the time. Ultimately, the computer player only has a strategy for building a winning position in the lowest amount of turns. If the opposing player can do it quicker, or starts sooner, the computer player has no strategy for stopping him. This is because the computer player isn’t affected by losses. If I implement some sort of negative reinforcement for losses, potentially this system could be sharpened up. Currently, I have no plans to move forward on this.
The creation of the winning positions list is a key element of this technique, and modifying what kinds of winning positions exist on this list can add all sorts of new functionality to JTT2. I mentioned previously about figuring a way to represent complex patterns by some sort of regular expression which seeks out position patterns with similar traits. This will require some work and, again, have have no plans to move forward on this.
On a more general note, the code for JTT2 could be better structured. If I were to move forward on one of the aforementioned plans, I am certain I would run into problems. Some elements of the code, especially determining new patterns and total game patterns, is spread out over several functions and depend heavily on where in the thread the functions are called. If I start changing things up, it would probably lead to a domino effect of functions no longer working. It would require major refactoring and take a lot of time.
Another shortcoming, again due to self-imposed time constraints, was my lack of testing. I have not written any tests for JakeTacToe 2.0. Any serious project worth moving forward on would be written along side of a slew of unit tests.
I’m excited to be finished with JakeTacToe. It was a great beginner’s project, but I think I stuck with it for too long. I should have moved onto something more personally interesting and useful which might have kept my interest long enough for me to put together something more professional.
In my next article, I want to write about what I’ve learned through JTT1 and JTT2; About the unforeseen challenges I came up against and about what I will do differently for my next project.